Professor Jia Li and colleagues have published a paper on high-quality magnetotransport in graphene using the edge-free Corbino geometry.

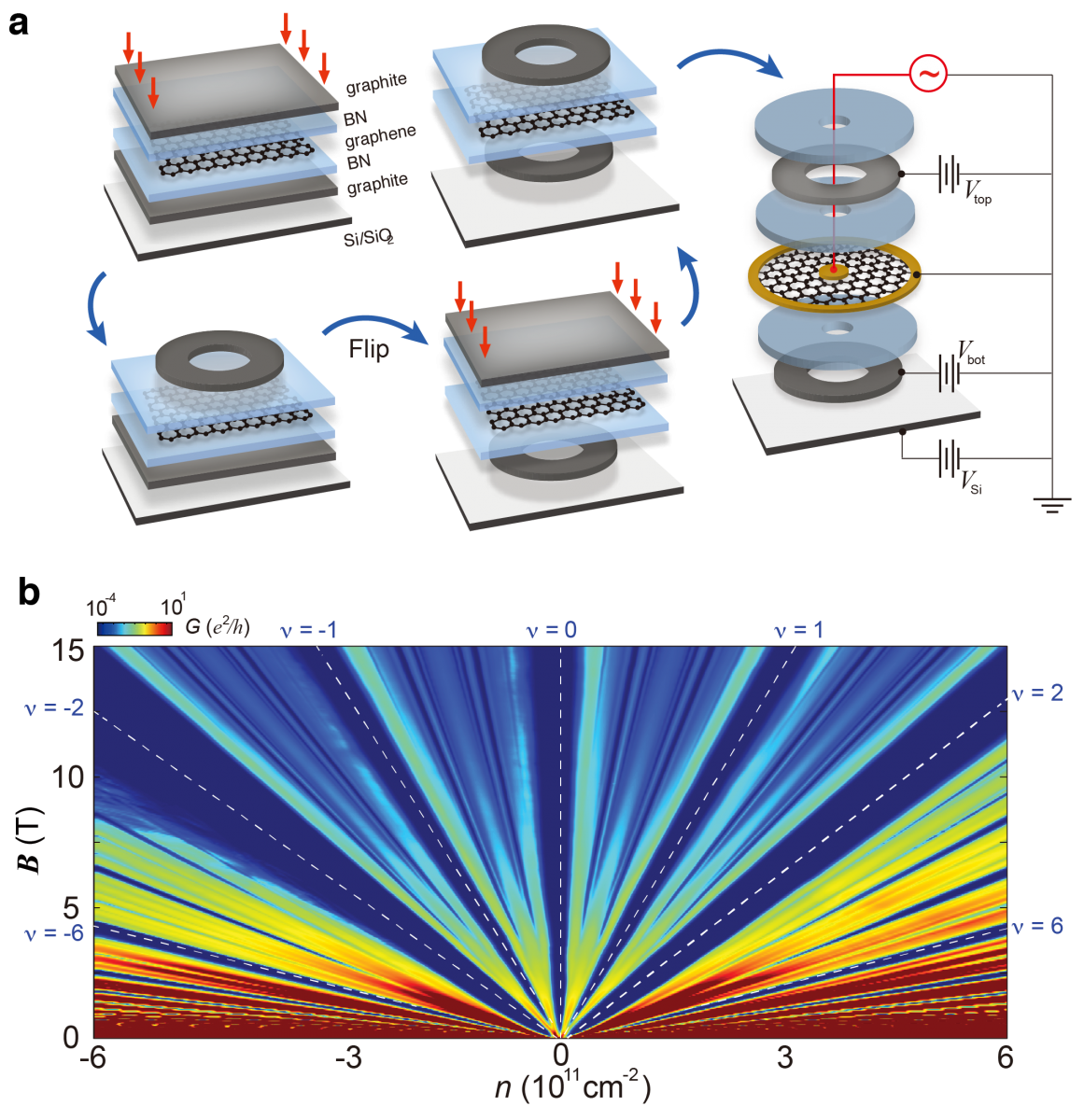
Geometry is important in studying topological phenomena of electrons in two-dimensional confinement, such as the quantum Hall effect. In a square shaped sample, current flow is concentrated on the physical edge. We can infer the property of sample interior by studying how electrons flow on sample edge (in a 2D sense). On the other hand, there is no physical edge connecting the inner and outer electrode in an anulus-shaped sample, making it possible to directly study the properties of sample interior with transport measurement.

In this paper, they report fabrication of graphene devices in a Corbino (anulus-shaped) geometry, consisting of concentric circular electrodes. They demonstrate that by probing transport through the bulk of the sample without the influence of edge channels, quantum Hall effect ground states can be identified to a degree that is unparalleled by conventional Hall bar (square-shaped) geometry. This is unexpected since it is generally assumed that QHE transport measurements are limited by bulk disorder and are otherwise insensitive to the device details.  By contrast, their results suggest that the QHE topological edge states in graphene may not be truly protected, or at least electron flow along the edge of Hall bar geometry, even with evidently good ohmic contact, does not provide, de facto, a robust probe of these states.   The observation lends new insight into a longstanding challenge in the development of graphene devices.